Típos de Wavelets

Você gostou do post,
e
quer mais?
Me paga um café! :) PIX consultoria@carlosdelfino.eti.br
Curta o post no final da página, use o Disqus, compartilhe em sua rede social. Isso me ajuda e motiva
Obrigado.

Hà vários formatos de wavelets, eles são categorizados a anotados conforme uso e formatos.

Abaixo listo alguns formatos e grupos sem entrar em muitos detalhes, cada um deles terá um artigo definindo a história e detalhes de uso, conforme for amadurecendo o assunto.

Haar Wavelets

O aprendizado sobre Wavelets devem começar pelo Haar Wavelet, que é um modelo simples, descontinuo e similar a uma função “step”, veja na imagem abaixo obtido no site do MathLab, como muitas utilizadas neste artigo.

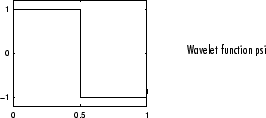
O Wavelet Haar é também citado como sendo o primeiro modelo do Wavelet Daubechies (db1).

Daubechies Wavelets

Ingrid Daubechies, Matemática que leciona na Universidade de Duke, dá o nome a esta série, ela é a maior e mais brilhante especialista da atualidade no tema.

Ingrid Daubechies, criou o que é chamado de *“Wavelets Ortogonais Compactadamente Suportados”* tornando assim a analise discreta viável.

Os Wavelets de Daubechies são nomeados usando duas letras e um número que define o nível do wavelets, assim usa-se as letras “db” seguido dos números, veja na imagem abaixo alguns Daubechs Wavelets, lembrando que o “db1” é o Haar Wavelet, a Mãe dos Wavelets.

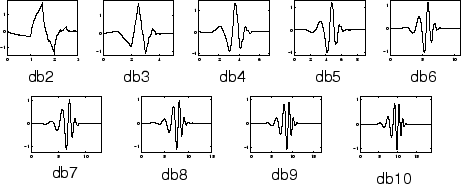
Biorthogonal Wavelets

Este típo de wavelet é importante para reconstruções de sinais e imagens, ela apresenta a propriedade de phases lineares. São usados dois wavelets, um para decomposição (o lado esquerdo) e o outro para reconstrução (o lado direito), ao invés de usar simplesmente um.

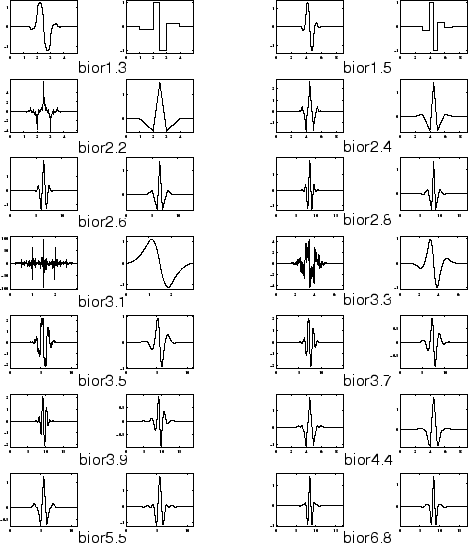
Coiflets Wavelets

Construído por I. Daubechies por solicitação de R. Coifman. Esta função wavelet tem 2N momentos igual a 0 e a função de escalonamento tem 2N-1 momentos iguais a 0. As duas funções tem um suporte de comprimento 6N-1.

Symlets

Os Symlets são wavelets aproximadamente simétricos propostos por I. Daubechies como modificação da familia db. As propriedades dos wavelets são similares entre as famílias.

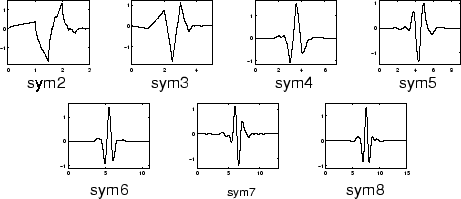
Morlet

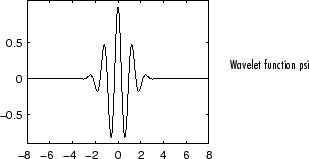
Mexican Hat

This wavelet has no scaling function and is derived from a function that is proportional to the second derivative function of the Gaussian probability density function. It is also knows as the Ricker wavelet.

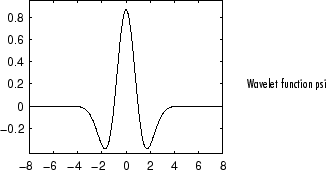
You can obtain a survey of the main properties of this family by typing waveinfo(‘mexh’) from the MATLAB command line. See Mexican Hat Wavelet: mexh in the Wavelet Toolbox User’s Guide for more information.

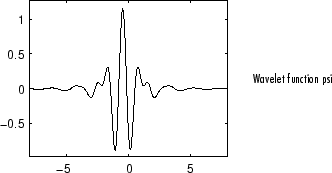
Meyer Wavelets

The Meyer wavelet and scaling function are defined in the frequency domain.

You can obtain a survey of the main properties of this family by typing waveinfo(‘meyer’) from the MATLAB command line. See Meyer Wavelet: meyr in the Wavelet Toolbox User’s Guide for more detail.