Aprendendo a Calcular Distâncias com base em coordenadas de GPS - Angulos menores que 7 graus

Transformar um par de coordenadas de GPS em um referência de distância não é complicado, neste artigo falo um pouco como fazer os cálculos para obter a distância entre dois pontos.

Revisado em: Janeiro de 2021.

O primeiro conceito que precisamos conhecer e entender bem para se converter pares de coordenadas de um GPS é a Milha Náutica.

A Milha Naútica

A Milha Náutica, que tem como simbolo comum NM do inglês Nautical Miles, é o equivalente a 1’ (um arco minuto) no grande circulo terrestre, ou seja considerando que se está no equador e que se movimente a fração de angulo de 1’ (um arco minuto) sobre o mar em direção sul ou norte, terá andando uma milha náutica, portanto: 1’ = 1NM`.

Na Inglaterra e Estado Unidos, apesar de não ser um sistema aceito oficialmente pelos órgãos normativos internacionais, ainda é usado uma medida chamada Milhas Terrestres, este sistema foi baseado na medida Romana de distância, onde 1000 passos dados por um centurião (Comandante de uma Milicia Romana), ou seja Mile Passus, passos que eram duplos com relação aos nossos passos normais e mediam o equivalente a 63360 polegadas, o que em metros mede 1851,85 metros, arredondando temos então 1852Mt.

No sistema inglês de medidas, uma Milha Náutica, 1.1508 milhas ou 6,076 pés.

Podemos calcular a Milha Geográfica que foi baseada em princípios científicos, considerando a terra redonda, qualquer linha a contorná-la terá 360 graus, porém sua superficie apresenta irregularidades. A linha do Equador mede aproximadamente 40.000Km, a medida feita por Eratostenes em 240 A.E.C., hoje a ciência comprovou que a medida não é muito diferente, sendo 40,075Km, ou seja, considerando que hoje sabemos que o raio da terra mede 6,378.14km, basta multiplicar este valor por $ 2 \times \pi $, assim teremos:

Vamos dividir então o comprimento da linha do equador (40,075km) por 360 graus e depois por 60 minutos (360° equivale a 60 minutos), teremos então a distância aproximada de de 1.851,85 mt para cada arco minuto (1’).

Assim fica claro que a cada 1’ (um minuto de arco) temos uma milha geografica que são 1855,33mt.

Porém a Milha Náutica oficial tem um valor bem próximo que é de 1852mt e foi definido em 1929 pela I Conferência Hidrográfica Internacional Extraordinária (First International Extraordinary Hydrographic Conference), realizada em Mónaco. O valor corresponde sensivelmente ao valor médio do comprimento de um minuto de arco do meridiano terrestre.

Na Marinha do Brasil se usa a equivalência 1 milha náutica = 2000 jardas = 6000 pés. O motivo desta equivalência é a utilização de radares com escalas em milhas e jardas, dependendo do alcance selecionado.

O que é longitude e latitude

Agora precisamos entender bem o que são Longitude e Latitude, veja que nosso intuito é didático portanto não entraremos profundamente na questão. Estaremos lidando com o conceito de coordenadas Geográficas com relação a curvatura da Terra, e devido a sua imperfeição teremos valores arredondados e aproximados do real.

Latitude é o ángulo entre o equador e uma determinada posição na terra quando nos movemos diretamente para um dos polos seja polo sul q ou polo norte, sendo o limite de cada polo o angulo de 90°, ou seja a distância entre os dois polos é de 180°. Representado pela letra grega φ. A terra é riscada para indicar latitudes especificas e de grande importância que são chamados de paralelos dentre os mais importantes temos:

• O Equador, divide a terra ao meio, tendo um lado o hemisfério sul, e do outro, o hemisfério norte.
• O trópico de Câncer é o trópico ao norte do equador terrestre, correspondendo ao paralelo 23.4378° (23º26’16”) de latitude norte. Junto com o equador, delimita a zona tropical norte.
• O trópico de Capricórnio é o paralelo situado 23.4378° ao sul do equador terrestre (23º26’16” de latitude sul). Delimita junto com o equador a zona tropical sul.
• O Círculo Polar Ártico terrestre corresponde ao paralelo da latitude 66º 33’ 44” (ou 66.5622°) Norte.
• Círculo Polar Antártico terrestres corresponde ao paralelo cuja latitude é 66º6/10 Sul e que corresponde ao complemento de 23º4/10 abatido nos trópicos.

Longitude é a distância em graus de qualquer ponto da Terra em relação ao Meridiano de Greenwich e também são conhecidas como meridianos.

As longitudes variam entre 0º e 180º para Leste(E) ou para Oeste(W), sendo contadas a partir do Meridiano de Greenwich.

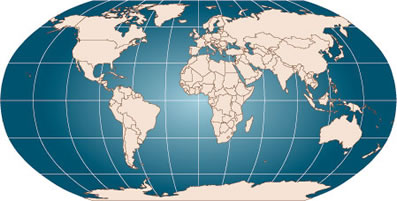
Mapa mundi, tipicamente seccionado em 15°, porém qualquer ponto da terra tem sua cordenada precisamente definida.

Apesar de as longitudes e latitudes serem traçadas cartograficamente a cada 15º, qualquer ponto da superfície terrestre possui latitude e longitude específicas, por isso usamos as medidas de 0 a 360°, que são divididas em arcos minutos, ou seja cada grau tem 60’ (60 arcos minutos), que também são divididos em 60 arco segundos (60”).

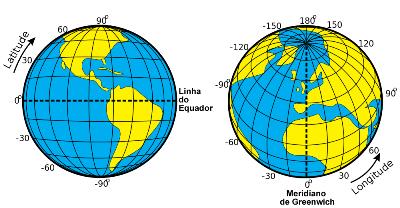
Latitude e Longitude apresendado no globo.

Calculando a Distâncias

Iremos discutir aqui três cenários, o primeiro distâncias pequenas, inferiores a 7° que se baseiam apenas na mudança de latitude ou longitude unicamente, depois distâncias pequenas, inferiores a 7° que tem variação de ambos, Latitude e Longitude. E o terceiro caso, grandes distâncias ou seja superior a 7°.

Há profissionais que consideram distâncias de até 14°, mas optaremos or 7° pois teremos uma maior precisão para distâncias acima deste valor.

A escolha deste angulo se dá pelo fato de percebermos facilmente a curvatura da terra quando já temos uma distância de 777,84Km.

Calculando Pequenas Distâncias com apenas a Latitude ou Longitude

Vamos começar fazendo o cálculo de distância entre dois pontos de forma simples, sem considerar a curvatura da terra. Vamos considerar dois Pontos A e B que variem apenas em sua Latitude:

Coordenadas do Estádio Castelão em Fortaleza, CE, a imagem permite visualizar as marcações usadas para cálculo do comprimento do estádio sua maior extenção.

• Ponto A
  • Longitude: 38°31’21.72”O
  • Latitude: 3°48’30.80”S
• Ponto B
  • Longitude: 38°31’21.72”O
  • Latitude: 3°48’21.28”S

Clicando nos links você poderá visualizar a posição do ponto marcado.

Devido a incompatibilidade de scripts, coloquei o Mapa de referência em outra página, para acessa-la clique aqui.

Neste caso, não precisamos nos preocupar com o par da coordenada, iremos trabalhar apenas com a parte do par de coordenadas que varia, no caso a Latitude, chamamos esta variação de DLA (distância Latitudinal).

Então aplicamos a fórmula para descobrir o DLA, onde $LA_F$ é a Latitude Final, e $LA_I$ é a Latitude Inicial:

Para medidas em graus decimais:

Para medidas em graus:

Como podemos ver o DLA é a distância em arco minutos, LAG, LAM e LAS são respetivamente, Graus da Latitude, Minutos da Latitude, Segundos da Latitude, todos em proporção ao Arco Minuto e devemos trabalhar com o módulo da distância, apenas usamos o sinal se desejarmos saber qual a direção que seguimos, o que não é o caso aqui, então considerando as duas latitudes informadas, 3°48’30.80”S e 3°48’21.28”S basta subtrai-las, individualmente para cada unidade, veja que quando a latitude é ao sul (S) usamos valores negativos, e quando a Longitude é a Oeste (O) usamos também valores negativos. Ficando assim nosso cálculo:

Agora temos nossa distância longitudinal em arco minuto, 0.1587, e assim podemos calcular quantos quilômetros temos de distância entre os dois pontos apenas multiplicando pelo relação existente de 1’ (Um arco minuto) para a Milha Marítima (1NM) que são 1852mt, então basta fazer a multiplicação final:

Como desejamos o cálculo em metros (mt) multiplicamos por 1852(mt), se quissemos em kilometros (Km) devemos usar 1.852(km).

Assim a distância entre o Ponto A e Ponto B no Estádio Castelão é de 293.91mt, vamos arredondar para 294mt. Ainda não podemos conferir se a distância está correta porque optamos em usar apenas uma das coordenada considerando que a outra está fixa, mas se formos ver na realidade o Castelão não está alinhado com meridiano, então a Longitude também altera.

Agore tente obter duas Longitudes e faça o mesmo cálculo, o principio é o mesmo.

Calculando Pequenas distâncias variando Longitude e Latitude

Ainda considerando que qualquer distância que varie menos de 7 graus não é necessário levar em consideração a curvatura da Terra, usaremos então apenas o cálculo da Hipotenusa para descobrirmos a distância entre os dois pontos quando se varia tanto a Longitude quando a Latitude, o cálculo é bem simples também Vejamos.

Basta fazermos o cálculo de cada distância separadamente pra começar, sendo assim calculamos o DLA (Distância Latitudinal) e DLO (Distância Longitudinal) seja em Metros ou Kilometros, em seguida calculamos a hipotenusa destas distâncias:

Lembre-se sempre que nestes calculos consideramos o Arco Minuto, não estamos lidando com graus.

Com isso obtemos a distância na medida escolhida. Vamos fazer um teste com dados reais. Como podemos ver a Longitude varia pouco no nosso exemplo, mas é o suficiente para termos um cálculo prático.

• Ponto A
  • Longitude: 38°31’21.72”O
  • Latitude: 3°48’30.80”S
• Ponto B
  • Longitude: 38°31’20.89”O
  • Latitude: 3°48’21.28”S

Clicando nos links você poderá visualizar a posição do ponto marcado.

Devido a incompatibilidade de scripts, coloquei o Mapa de referência em outra página, para acessa-la clique aqui.

Agora que temos o DLO e o DLA calculamos a hipotenusa.

A diferença no valor em relação ao outro cálculo é pequena devido a pequena inclinação Longitudinal.

Vejam no Google Maps se está certo medindo a distância entre os dois pontos. Poderá haver pequenas diferenças de até 50 metros, uma vez que os pontos não estão 100% sincronizados.

Cálculo para Grandes Distâncias

O Calculo de grandes distâncias, principalmente longe dos grandes círculos, ou seja proximos ao equador e aos trópicos demandam cálculos bem mais complexos que estão sendo anotados no artigo Calculando grandes distâncias com base em coordenadas de gps - distancias maiores que 7 graus

Verificando o resultado de seus calculos

Para reduzir o número de scripts e o tamanho da página dividi este artigo em outros, assim o script de teste e calculo foi transferido para o artigo:

Fontes:

• http://edwilliams.org/ellipsoid/ellipsoid.pdf
• http://www.inaccess.com.br/?p=1163

• https://www.lapintagalapagoscruise.com/blog/nautical-miles-vs-miles/#:~:text=A%20nautical%20mile%20is%20based,Earth%20is%201%20nautical%20mile.

• https://www.wolframalpha.com/

• https://mundoeducacao.uol.com.br/geografia/latitudes-longitudes.htm
• http://mundoestranho.abril.com.br/materia/por-que-a-milha-nautica-ediferente-da-milha-terrestre
• https://super.abril.com.br/mundo-estranho/por-que-a-milha-nautica-e-diferente-da-milha-terrestre/
• https://pt.wikipedia.org/wiki/Milha_n%C3%A1utica
• https://pt.wikipedia.org/wiki/Tr%C3%B3pico
• https://pt.wikipedia.org/wiki/C%C3%ADrculo_Polar_%C3%81rtico
• https://pt.wikipedia.org/wiki/C%C3%ADrculo_Polar_Ant%C3%A1rtico
• https://en.wikipedia.org/wiki/Mendenhall_Order
• http://www.pilotopolicial.com.br/calculando-distancias-e-direcoes-utilizando-coordenadas-geograficas/
• http://www.gpsy.com/gpsinfo/

Não deixe de me pagar um café, faz um PIX: consultoria@carlosdelfino.eti.br de qualquer valor.