e
quer mais?
Me paga um café! :) PIX consultoria@carlosdelfino.eti.br
Curta o post no final da página, use o Disqus, compartilhe em sua rede social. Isso me ajuda e motiva
Obrigado.
Abaixo uma coleção de funções que podem ser usadas para construção de redes neurais, aqui apresento as principais funções, e discutirei posteriormente o melhor uso de cada uma.
Abaixo apresentaremos alguns funções muito importante para a compreensão de como funciona as redes neurais, as funções do tipo degrau podem ser usadas para ativar ou desativar um grupo de neurônios, por exemplo.
Já as funções logística e tangente hiperbólicas podem ser usada também no processo de ativação e desativação de redes mais complexas como LTSM, que veremos mais no final desta série de postagens.
Temos também as funções Gaussianas são usadas em sistemas neurais que determinam um ponto central de classificação com base em uma média e a Função linear, é a mais simples de todas e são usadas em redes neurais para nivelar sinais para se equiparar níveis de entradas, como um sistema de acoplamento, elas podem ter entradas e saídas com valores iguais ou proporcionais direta ou inversamente.
Na próxima postagem veremos os tipos de redes neurais existentes, tanto a nível de funções como arquitetural e como estas funções podem ser aplicadas nelas.
As funções do tipo degrau.
Há funções simples do tipo degrau conhecidas do inglês como Heavyside/band limiter, são funções com algorítimos de tomada de decisão bem simples baseada em um IF por neurônio, sendo o valor potencial da sinapse maior que zero provoca assim a ativação do neurônio, ou mesmo duas faixas limites quando for uma função degrau bipolar ou função sinal também conhecida do inglês de Symmetric board limiter, a ativação tendo dois estágios, um positivo outro negativo.
Para degrau simples temos:
\[f(x) = \begin{cases} 1, \text{se} \; x \ge 0 \\ 0, \text{se} \; x \lt 0 \end{cases}\]Já para degrau bipolar temos:
\[f(x) = \begin{cases} 1, \text{se} \; x \ge 0 \\ 0, \text{se} \; x == 0 \\ -1, \text{se} \; x \le 0 \end{cases}\]No uso da função degrau bipolar é possível aproveitar o ultimo valor obtido informado no algorítimo que a função mantem este valor inalterado caso o valor atual na sinapse é igual a zero.
Há também a possibilidade de resumir a função degrau bipolar de forma a ficar conforme abaixo:
\[f(x) = \begin{cases} 1, \text{se} \; x \ge 0 \\ -1, \text{se} \; x \gt 0 \end{cases}\]Função Rampa
Uma outra amadurecimento da função degrau bipolar é a função rampa, que é presentada pela função:
\[f(x) = \begin{cases} l, \text{se} \; x \gt l \\ x, \text{se} \; -l \le x \le l \\ -l, \text{se} \; x \lt -l \end{cases}\]Neste caso tanto o valor \(l\) é ajustado conforme os limites desejados para a rampa.
Funções totalmente diferenciáveis.
Temos 4 funções diferenciáveis que podem ser usadas como solução para nossos neurônios, tais funções são apresentadas abaixo e possuem suas diferenciais de primeira ordem conhecidas em todos os pontos de domínio de definição.
Função Logística
\[f(x) = \frac{1}{1+e^(-\beta*x)}\]Na formula acima e é o número de euler portanto $e= 2.718281828459045235360287$, e \(\beta\) é uma constante que ajusta a inclinação da curva, veja o gráfico baixo, onde o segundo parâmetro o que vai após o ponto e virgula é o valor de \(\beta\).
| x | f(x;.01) | f(x;0.02) | f(x;0.03) | f(x;0.04) | f(x;0.05) |
|---|---|---|---|---|---|
| -1.000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| -900 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| -800 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| -700 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 |
| -600 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 |
| -500 | 0,007 | 0,000 | 0,000 | 0,000 | 0,000 |
| -400 | 0,018 | 0,000 | 0,000 | 0,000 | 0,000 |
| -300 | 0,047 | 0,002 | 0,000 | 0,000 | 0,000 |
| -200 | 0,119 | 0,018 | 0,002 | 0,000 | 0,000 |
| -100 | 0,269 | 0,119 | 0,047 | 0,018 | 0,007 |
| 0 | 0,500 | 0,500 | 0,500 | 0,500 | 0,500 |
| 100 | 0,731 | 0,881 | 0,953 | 0,982 | 0,993 |
| 200 | 0,881 | 0,982 | 0,998 | 1,000 | 1,000 |
| 300 | 0,953 | 0,998 | 1,000 | 1,000 | 1,000 |
| 400 | 0,982 | 1,000 | 1,000 | 1,000 | 1,000 |
| 500 | 0,993 | 1,000 | 1,000 | 1,000 | 1,000 |
| 600 | 0,998 | 1,000 | 1,000 | 1,000 | 1,000 |
| 700 | 0,999 | 1,000 | 1,000 | 1,000 | 1,000 |
| 800 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 |
| 900 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 |
| 1.000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 |
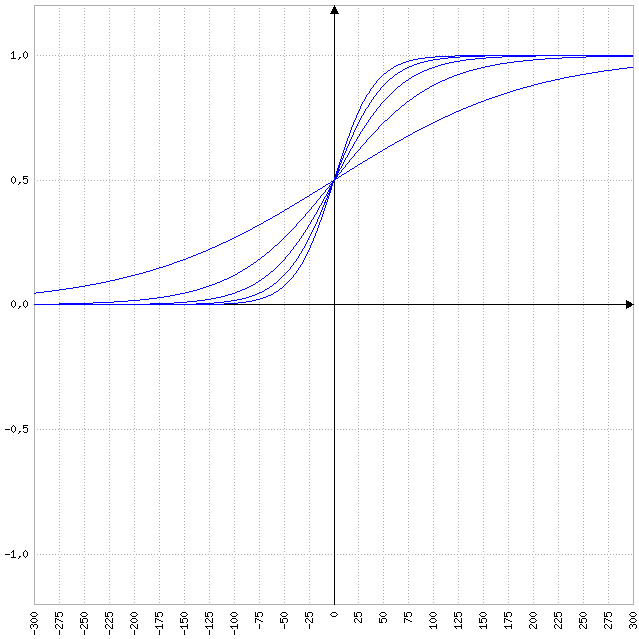
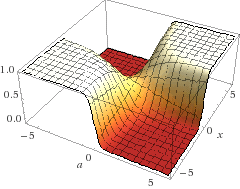
No gráfico abaixo apresento a mesma função em um formato tridimensional, onde o eixo z é a variação das alternativas para \(\beta\).
Função Tangente Hiperbólica
\[f(x) = \frac{1-e^(\beta*x)}{1+e^(\beta*x)}\]Na fórmula acima e é o número de Euler, \(e= 2.718281828459045235360287\), e \(\beta\) é uma constante que ajusta a inclinação da curva, veja o gráfico a baixo, onde o segundo parâmetro o que vai após o ponto e vírgula é o valor de \(\beta\).
| x | f(x;.01) | f(x;0.02) | f(x;0.03) | f(x;0.04) | f(x;0.05) |
|---|---|---|---|---|---|
| -1.000 | -1,000 | -1,000 | -1,000 | -1,000 | -1,000 |
| -900 | -1,000 | -1,000 | -1,000 | -1,000 | -1,000 |
| -800 | -0,999 | -1,000 | -1,000 | -1,000 | -1,000 |
| -700 | -0,998 | -1,000 | -1,000 | -1,000 | -1,000 |
| -600 | -0,995 | -1,000 | -1,000 | -1,000 | -1,000 |
| -500 | -0,987 | -1,000 | -1,000 | -1,000 | -1,000 |
| -400 | -0,964 | -0,999 | -1,000 | -1,000 | -1,000 |
| -300 | -0,905 | -0,995 | -1,000 | -1,000 | -1,000 |
| -200 | -0,762 | -0,964 | -0,995 | -0,999 | -1,000 |
| -100 | -0,462 | -0,762 | -0,905 | -0,964 | -0,987 |
| 0 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 100 | 0,462 | 0,762 | 0,905 | 0,964 | 0,987 |
| 200 | 0,762 | 0,964 | 0,995 | 0,999 | 1,000 |
| 300 | 0,905 | 0,995 | 1,000 | 1,000 | 1,000 |
| 400 | 0,964 | 0,999 | 1,000 | 1,000 | 1,000 |
| 500 | 0,987 | 1,000 | 1,000 | 1,000 | 1,000 |
| 600 | 0,995 | 1,000 | 1,000 | 1,000 | 1,000 |
| 700 | 0,998 | 1,000 | 1,000 | 1,000 | 1,000 |
| 800 | 0,999 | 1,000 | 1,000 | 1,000 | 1,000 |
| 900 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 |
| 1.000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 |
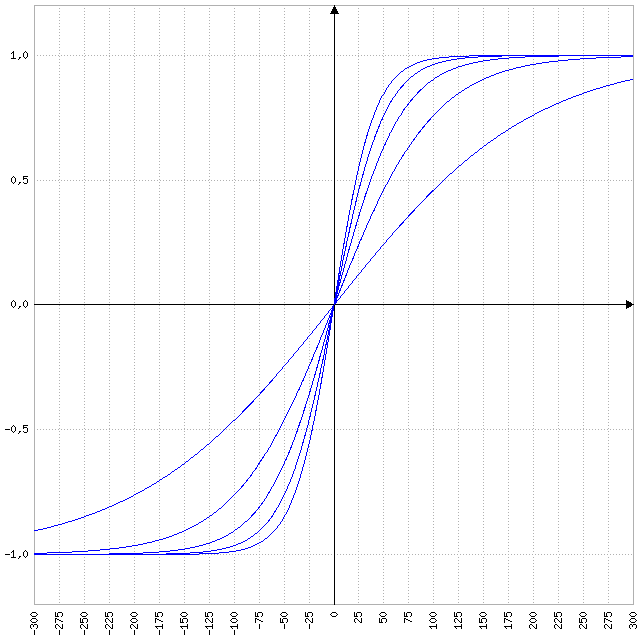
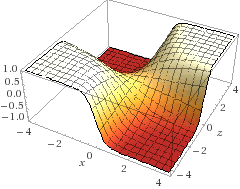
No gráfico abaixo apresento a mesma função em um formato tridimencional, onde o eixo z é a variação das alternativas para \(\beta\).
Função Gaussiana
\[f(x) = e ^ { - { \frac{(x - c)^2}{2 \; * \; \sigma^2 } } }\]| x | f(x;-10) | f(x;-2) | f(x;6) |
|---|---|---|---|
| -1.000 | 0,000 | 0,000 | 0,000 |
| -900 | 0,000 | 0,000 | 0,000 |
| -800 | 0,000 | 0,000 | 0,000 |
| -700 | 0,000 | 0,000 | 0,000 |
| -600 | 0,000 | 0,000 | 0,000 |
| -500 | 0,000 | 0,000 | 0,000 |
| -400 | 0,000 | 0,000 | 0,000 |
| -300 | 0,000 | 0,000 | 0,000 |
| -200 | 0,000 | 0,000 | 0,000 |
| -100 | 0,000 | 0,000 | 0,000 |
| 0 | 0,801 | 0,991 | 0,923 |
| 100 | 0,000 | 0,000 | 0,000 |
| 200 | 0,000 | 0,000 | 0,000 |
| 300 | 0,000 | 0,000 | 0,000 |
| 400 | 0,000 | 0,000 | 0,000 |
| 500 | 0,000 | 0,000 | 0,000 |
| 600 | 0,000 | 0,000 | 0,000 |
| 700 | 0,000 | 0,000 | 0,000 |
| 800 | 0,000 | 0,000 | 0,000 |
| 900 | 0,000 | 0,000 | 0,000 |
| 1.000 | 0,000 | 0,000 | 0,000 |
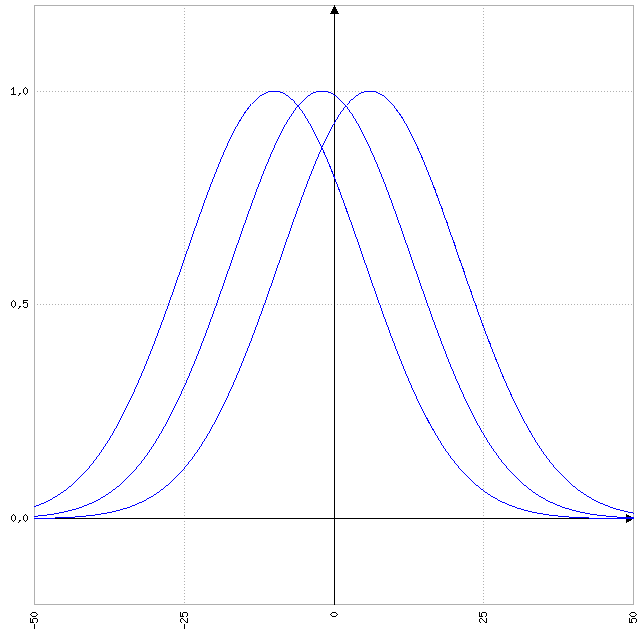
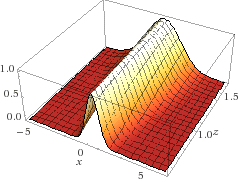
No gráfico abaixo temos a mesma função em um formato tridimensional, onde o eixo z é a variação da posição do eixo central z, \(\sigma\) foi mantido fixo no valor 1.
Função Linear
\[f(x) = x\]A função linear pode ser do tipo identidade como na fórmula acima, ou pode ser proporcional, sendo seu objetivo acoplar a saída de uma rede neural a outra rede, compatibilizando nível de valores:
\[f(x) = x * \sigma\]Neste caso \(\sigma\) será o fator de multiplicação para nivelar os sinais da rede.
No próximo post comento um pouco sobre as Redes do tipo Perceptron.
Caso esteja buscando aprender mais e compartilhar conhecimento, participe de nosso grupo no facebook: Artificial Intelligence and Neural Network
Wavelets
Arquiteturas
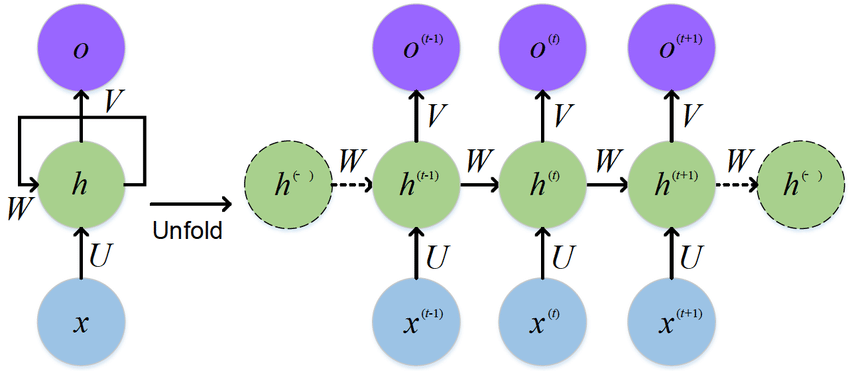
RNN
Recorrente Neural Network
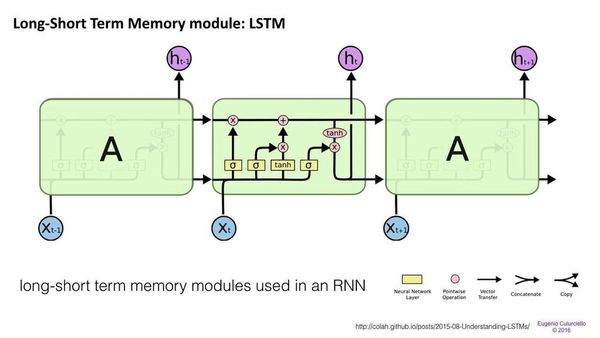
LTSM
Long Short-term Memory ou Memória de longo Prazo é uma arquitetura de rede neural artificial recorrente (RNN) usada em Deep Learning. Ao contrário das redes neurais de avanço padrão, o LSTM possui conexões de feedback. Ele não pode apenas processar pontos de dados únicos, mas também sequências inteiras de dados.
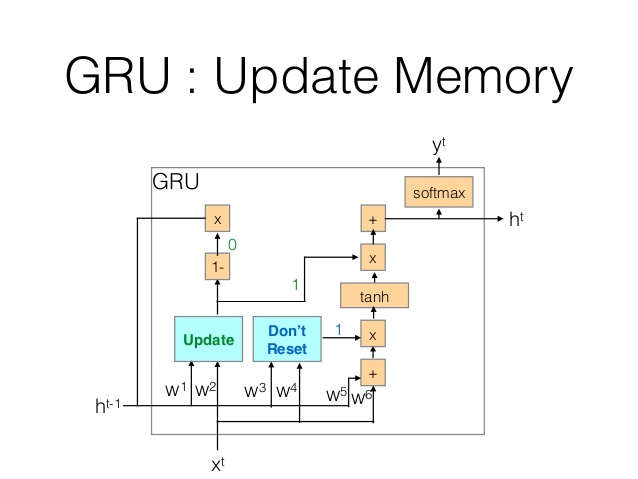
GRU
AE
VAE
DAE
SAE
RBM
MC
HN
BM
DBM
DCNN
DN
DCIGN
GANS
LSM
ELM
ESN
DRN
KN
NTM
Ferramentas usadas para construir os gráficos
Nos links abaixo estão as ferramentas utilizadas para construir as formulas e gráficos, além de gerar os dados.
- http://developer.wolframalpha.com/widgetbuilder/?_ga=1.243513221.1439349164.1470078370
- http://www.mathe-fa.de/pt#result
- http://detexify.kirelabs.org/classify.html
- http://meta.math.stackexchange.com/questions/5020/mathjax-basic-tutorial-and-quick-reference
- https://domchristie.github.io/to-markdown/
Não deixe de me pagar um café, faz um PIX: consultoria@carlosdelfino.eti.br de qualquer valor.
