Introdução aos Wavelets

Você gostou do post,
e
quer mais?
Me paga um café! :) PIX consultoria@carlosdelfino.eti.br
Curta o post no final da página, use o Disqus, compartilhe em sua rede social. Isso me ajuda e motiva
Obrigado.

Wavelets são formas de onda efetivamente limitadas num curto espaço de tempo, que tem uma média de valores entre zero e não zero.

Revisado em 27/12/2021

Wavelets tendem a ser irregulares, não mantem uma recorrência como sinais senoidais ou composições de sinais senoidais, como proposto pelas Analises de Furrier. Porém, pode ser que algum sinal seja composto pela repetição de wavelets, o que pode gerar um pouco de confusão, mas vamos tentar entender um pouco isso abaixo.

Bem, se você está procurando a Banda Wavelets, não iremos falar dela aqui, você pode obter mais informações neste link, mas acho que ela se aposentou. Não poderia deixar de cita-la.

Na categória wavelets você vai encontrar todas as anotações que eu tenho feito sobre o tema.

Estou trabalhando nestas anotações, estudos retomados em 13/01/2020. E novamente retomado em 27/12/2021.

Motivação

Meus estudos com Wavelets se deram mais intensos em 2017, quando comecei a busca de um algoritmo para detecção e analise de sinais de ECG (Eletrocardiograma), eu precisava além de identificar a pulsação do coração, identificar suas condições médicas através dos sinais obtidos. O sinal é coletado com o chip BMD101, um chip especializado da NeuroSky para coleta de ECG, porém precisava de mais detalhes, e com os dados puros (RAW) do ECG poderia fazer a analise, inicialmente pensei em usar Transformatas de Fourrier, porém, me pareceu muito pesado e inadequado para o uso, apesar de muitos indica-la como sendo o caminho.

De certa forma era o caminho, delas cheguei aos Wavelets, pequenas amostragens vetoriais e ortogonais que representam um formato de onda que desejo obter na amostragem, através do wavelets poderia procurar a “agulha no palheiro”, ou seja aqueles pulsos que demonstram que algo está errado no coração, saber a taxa de pulsação do coração não seria suficiente, eu precisava saber de sua variabilidade e também a deformação de tais pulsos, além de a presença de outros pulsos que poderiam sugerir outras anormalidades.

O Wevelets me pareceu ser o caminho, ele me ajudaria de forma discreta e com um algoritmo rápido achar pulsos que estejam fora do comum, mas parece que falta algo mais, e não só dominar o tema seria suficiente.

Bem o projeto já não está mais sobre minha responsabilidade, mas minhas pesquisas continuam, e eu tenho buscado agora retomar os estudos especificamente sobre wavelets de forma geral, e entender sua aplicação e como construir novos algoritmos com base no contexto aplicado.

Preparando o Ambiente

Para desenvolver tal estudo, eu precisei preparar minha estação de trabalho, inicialmente com dois software, o Octave e o VScode, o primeiro é uma ferramenta simulações e calculos matemáticos similar ao Mathlab que permite desenvolver scripts matemáticos, produzida pela projeto GNU é Open Source e gratuita, muito útil para o estudo e avanço no domínio da matemática, o segundo talvez mais conhecido é uma IDE aberta produzida pela Microsoft que permite integrar plugins e ferramentas como o Octave, entre muitas outras. Para usar o Octave junto com o VScode usei o plugin disponível neste link](https://marketplace.visualstudio.com/items?itemName=toasty-technologies.octave). Porém o editor “VI” pode também ser usado sem integração. O próprio Octave pode ser usado como editor através de sua interface de usuário grafica.

Para instalar ambas as ferrametnas use os links abaixo, ou então as ferramentas de instalação do sistema operacional que usa.

Bem, instale ambos os programas, depois dentro do VSCode instale o plugin, não irei entrar em detalhes quanto a esta instalação.

Para usar o Octave no Linux o processo de instalação pode ser diferente, não irei entrar em detalhes para este processo de instalação, mas farei algumas anotações no Instalando Octave no Linux.

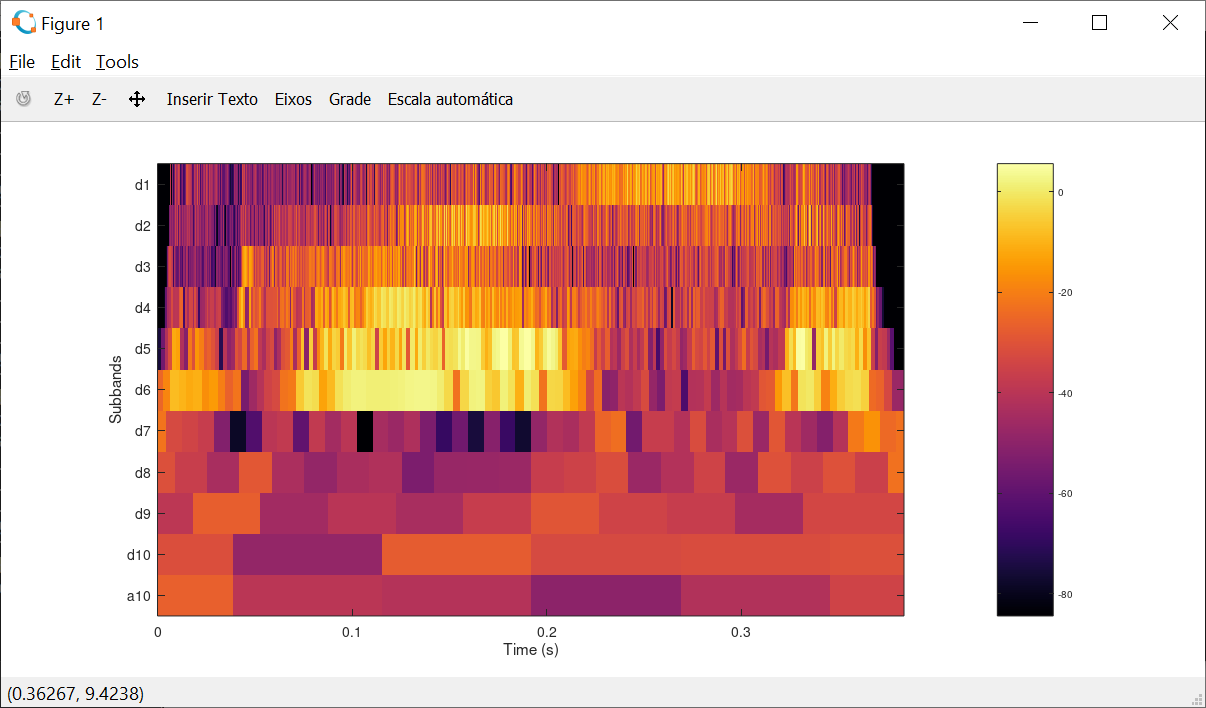
Um exemplo simples de uso da função FWT para wavelet 'db8'

A imagem acima é obtida usando o script a seguir:

    pkg load ltfat
    [f,fs] = greasy;
    J = 10;
    [c,info] = fwt(f,'db8',J);
    plotwavelets(c,info,fs,'dynrange',90);

Para darmos continuidade, será preciso instalar alguns toolbox no Octave. Iremos inicialmente instalar o Signal Processing, este toolbox possui divresas funções que auxiliam em DPS e o LTFAT - Larger Timer/Frequency Analise Tools, um toolbox que pode ser usado tanto para pesquisas acadêmicas como profissionais.

Para instalar ambos é muito simples abra o Octave Cli, e execute o seguinte comando, atenção a detalhes no linux apresetado no artigo acima:

pkg install signal ltfat

conforme o desempenho de sua estação de trabalho e de sua internet irá demorar alguns minutos e assim que terminar, correndo tudo bem, execute os seguintes comandos para ver uma Wavelet do tipo morlet:

pkg load signal

lb = -4;
ub = 4;
n = 1000;
[psi,xval] = morlet(lb,ub,n);
plot(xval,psi,"linewidth",4)
grid on

Os comandos acima executam o seguinte, primeiro carrega o toolbox Signal Processing. Declara três variáveis chamadas, lb, ub, n respectivamente, então chama a função morlet que irá gerar uma estrutura com os dados para reconstrução visual do Wavelet do tipo Morlet,, finalmente é chamado a função que irá plotar gráficamente o nosso Wavelet com o grid ligado no gráfico. (veja em referências onde obtive o exemplo.)

Como pode ver se você já tem alguma noção de programação, é bastante intuitivo. Teremos o seguinte resultado:

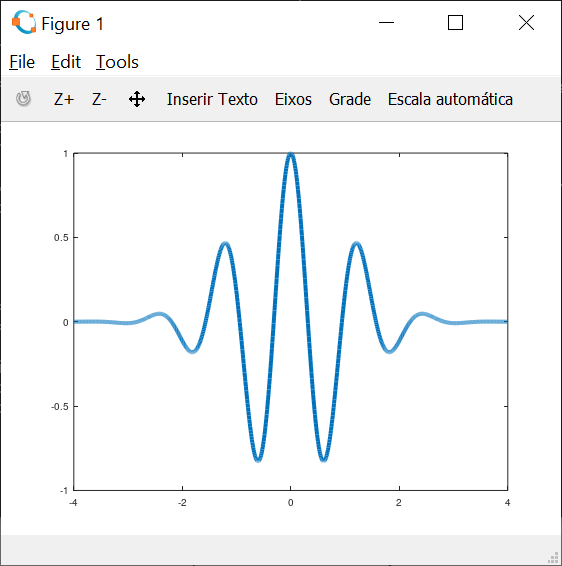
Morlet Wavelet

Para mais funções veja este link.

Vamos fazer mais um teste com o Wavelet Mexican Hat](http://carlosdelfino.eti.br/matematica/wavelets/mexican_hat-wavelets/), basta mudarmos a função:

[psi,xval] = mexihat(lb,ub,n);
plot(xval,psi,"linewidth",4)
grid on

Então teremos o seguinte resultado:

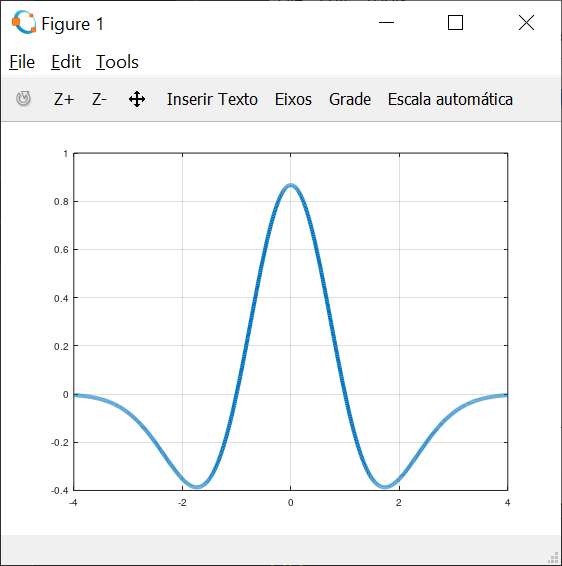
Mexican Hat Wavelet

Para mais detalhes sobre ferramentas clique aqui.

Arbitrário

que não segue regras ou normas; que não tem fundamento lógico; que apenas depende da vontade ou arbítrio daquele que age.

Wavelets são funções arbitrárias, ou seja você pode adotar a função que quiser para definir seu formato de onda, apenas é preciso se atendar para que seja uma representação real de uma janela de amostragem.

Wavelets tem assim uma número infinito de transformações (Transformatas);

Conclusão

Este post é apenas um de muitos que precisam ser concluidos e serão postados aqui, o próximo post a ser visto é o http://carlosdelfino.eti.br//matematica/wavelets/wavelets_octave_entre_outros/)