Números Imaginários

O que São Números Imaginários

Como todos sabem eu me formei no supletivo em 1998, o que me trouxe uma grande lacuna na minha formação matemática, eu até avanço bem em muitos conceitos matemáticos, porém muitas vezes escorrego e preciso rever alguns estudos, e agora estou revendo os cálculos com números complexos para me aprofundar nos estudos em Analise de “Sistemas e Sinais” no livro do Alan V. Oppenheim, “Signals and Systems”.

O Material abaixo é uma tradução livre, acrecido com meus textos e observações, do conteúdo do site Milefoodt Matematics - Imaginary Numbers.

O que é $\sqrt{-1}$? Um simbolo imposto aos terraqueos por uma cultura alienigena? bem, não exatamente … (a menos que você veja a matemática como representante de uma cultura aliem … mas não vamos por ai).

Os numeros “usuais” por pessoas “normais” são chamados números reais. Eles incluens todos os números, frações, decimais, números negativos, raizes quadradas de números positivos, e números como pi (3.14159265…). Eles incluem basciamente qualquer que seja calculado em torno de uma decimal, ou qualquer que seja posicionado em uma linha númerica.

Mas, $\sqrt{-1}$ não tem uma posição na linha de números, não há um número que possamos obter o quadrado de um negativo. o quadrado de um número positivo sempre produz um número positivo, e o quadrado de um número positivo sempre produz um número positivo. Portanto, como nos temos um quadrado de um número negativo?

resposta: Nos não podemos usar um número real $\sqrt{-1}$. Nós devemos usar um típo diferente de número. Os matemáticos do século dezeseis que primeiro trabalhou com seriédade sobre $\sqrt{-1}$ não tinha certeza de qual o seu significado, então o chamaram de número imaginário, sendo um termo muito infeliz. não havendo nada imaginário sobre $\sqrt{-1}$. (mas demorou dois séculos para que os matemáticos em geral entendessem eu significado).

Hoje, nós costumamos usar o símbolo i para representar $\sqrt{-i}$. Matemáticos usam um das duas declarações como definção de i, ou $i=\sqrt{-1}$ ou $i²=-1$. (alguns engenheiros eletricos usaram j no lugar de i, porque eles usam i para representar a força de indução, ou seja corrente. mas a ideia é a mesma.)

Nos não precisamos outra definição para raiz quadrada de outros números, tendo i é suficiente. Por insntante, nos escrevemos $\sqrt{-9} = 3i$, desdeque a raiz de 9 é 3, e a raiz quadrada de um número negativo produzirá um número i.

Classificando os Novos Típos de Números

A coleção de números criados para agrupar as raizes quadradas de números negativos são algumas chamados de números puramente imaginários. Em símbolos, nós podemos escrever como um números puramente imaginários genericos como bi, o produto de um número real não zero b com o número imaginário i.

Nenhum dos números imaginários tem uma posição na linha de números.

Nos podemos também falar sobre adição de um número real com um número puramente imaginário. O resultado é chamado de um número complexo. Em símbolos, um número complexo, são números no formato $a + bi$, onde asão números reais, e bisão números puramente imabinários.

Se estes números não estão na linha de números, nós podemos podem desenhar uma figurade números complexo ou números imaginários? Atualmente, sim. Mas uma linha de números de uma dimensão não será suficiente. Um número imaginário puramente complexo precisa ser representado em uma segunda linha de números. Em outras palavras, nos precisamos de duas linhas dimencionais para trazer uma figura que representa os números compleox. Aqui está uma figura de um número $2+3i$ representado por um ponto.

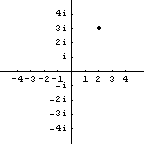
Portanto, os números reais são pontos nos eixos horizontais. Números imaginários aqueles números que não são reais e estão localizados em algum lugar diferente do eixo horizontal. Números puramente imaginários são pontos no eixos verticais (diferentes da origem). Números complexos incluem todos as possiblidades na figura. (Números reais são números complexos. Também são número imaginários. Assim como todo número é uma fração.)

Conclusão

Vimos que j não passa de um apelido para i no contexto da engenharia eletrica, para não ser confundido com o símbolo da corrente elétrica, também, não precisamos de uma nova dimensão para representar os números complexos.

Isso é só o inicio, agora você pode ver um pouco mais sobre Raiz Quadara de i, no próximo artigo.

Não deixe de me pagar um café, faz um PIX: consultoria@carlosdelfino.eti.br de qualquer valor.